Heap and Priority Queue

First we should know about “Complete Binary Tree” as we will use later.

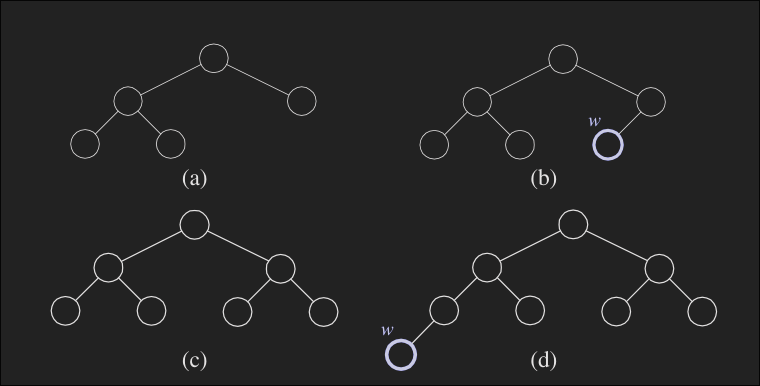
Complete Tree

Complete binary tree is a binary tree where all of its level are filled completely (perfect) except the last level is filled from left to right. A binary tree is perfect if all parent nodes have two children and all leaves are on the same level. The level of a node is the number of edges along the path between it and the root node.

We’ll represent it as an array such that at index 1 is the root, this is the code:

template <typename E> class completeTree {
public:
  typedef typename vector<E>::iterator Position;

  completeTree() : v(1) {}

  int size() const { return v.size() - 1; }

  Position left(const Position &p) { return pos(2 * idx(p)); }
  Position right(const Position &p) { return pos(2 * idx(p) + 1); }
  Position parent(const Position &p) { return pos(idx(p) / 2); }

  bool hasLeft(const Position &p) const { return 2 * idx(p) <= size(); }
  bool hasRight(const Position &p) const { return 2 * idx(p) + 1 <= size(); }
  bool isRoot(const Position &p) const { return idx(p) == 1; }

  Position root() { return pos(1); }
  Position last() { return pos(size()); }

  void addLast(const E &e) { v.push_back(e); }
  void removeLast() { v.pop_back(); }

  void swap(const Position &p, const Position &q) { std::swap(*p, *q); }

  Position pos(int i) { return v.begin() + i; }
  int idx(const Position &p) const { return p - v.begin(); }

private:
  vector<E> v;
};

Heap

A heap is a binary tree such that its root is the minimum or maximum or any compare function we choose. The root is less than its children.

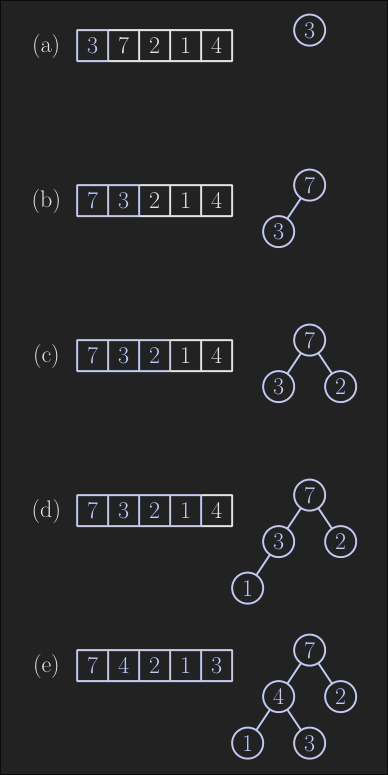
Bottom-Up Heap construction

template <typename E, typename C>
void buildHeap(vector<E> &v) { // 0-index
  C isLess = C(); // compare function (class with () overload, see below)
  // Heapify for the opposite of isLess (Heap for the max if isLess was for min)
  auto heapify = [&v, &isLess](int idx) -> void {
    int n = v.size();
    while (2 * idx + 1 < n) {
      int mnIdx = 2 * idx + 1;
      int rightIdx = 2 * idx + 2;
      if (rightIdx < n && isLess(v[rightIdx], v[mnIdx])) {
        mnIdx = rightIdx;
      }
      if (isLess(v[mnIdx], v[idx])) {
        swap(v[idx], v[mnIdx]);
        idx = mnIdx;
      } 
      else break;
    }
  };
  // Build the heap
  for (int i = (n - 1) / 2; i >= 0; i--) {
    heapify(i, n);
  }
}
// comparer
class smaller {
public:
  bool operator()(const int &a, const int &b) const { return a < b; }
};

Heap Sort

To sort an array we just need to extract the heap we’ve just built, as the root is the minimum we’ll swap it with the last element. Now the root may be not the minimum right ? heapify.. Now the current root is the next minimum, swap it with the the last-1 element and heapify and so on.

Note: it’s !isLess not isLess because we want to sort in ascending order (max at last), so we’ll use a max heap not a min heap (root is the max).



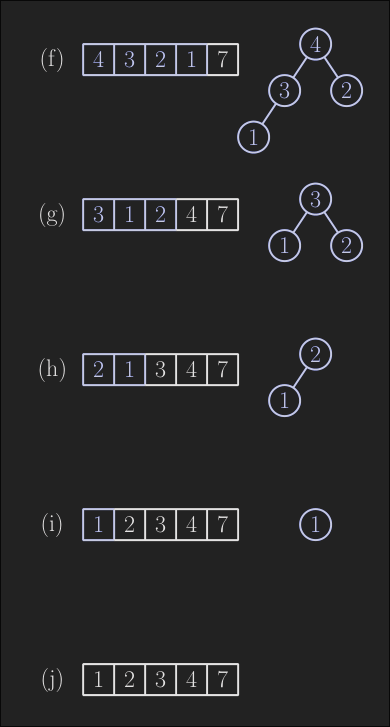
This is the full heapSort function:

template <typename E, typename C> void heapSort(vector<E> &v) {
  C isLess = C();
  int n = v.size();
  // Heapify for the oposite of isLess (Heap for the max if isLess was for min)
  auto heapify = [&v, &isLess](int idx, int n) -> void {
    while (2 * idx + 1 < n) {
      int mnIdx = 2 * idx + 1;
      int rightIdx = 2 * idx + 2;
      if (rightIdx < n && !isLess(v[rightIdx], v[mnIdx])) {
        mnIdx = rightIdx;
      }
      if (!isLess(v[mnIdx], v[idx])) {
        swap(v[idx], v[mnIdx]);
        idx = mnIdx;
      } else {
        break;
      }
    }
  };
  // Build the heap
  auto build = [&v, &n, heapify]() -> void {
    for (int i = (n - 1) / 2; i >= 0; i--) {
      heapify(i, n);
    }
  };
  build();
  // Extract elements from the heap
  for (int i = n - 1; i > 0; i--) {
    swap(v[0], v[i]);
    heapify(0, i);
  }
}

You can try this function in any sorting problem online (LeetCode, Codeforces, etc).

Priority Queue

Priority queue is just a heap with keeping the heap property as we insert new elements or remove them.

template <typename E, typename C> class HeapPriorityQueue {
public:
  HeapPriorityQueue() : isLess(C()) {}
  HeapPriorityQueue(const vector<E> &v) : isLess(C()) {
    for (auto &i : v) {
      insert(i);
    }
  }

  int size() const { return T.size(); }
  bool empty() const { return size() == 0; }
  const E &min() { return *T.root(); }

  // Insert as last and heapify up until its right place
  void insert(const E &e) {
    T.addLast(e);
    Position nd = T.last();
    while (!T.isRoot(nd)) {
      Position par = T.parent(nd);
      if (isLess(*nd, *par)) {
        T.swap(par, nd);
        nd = par;
      } else {
        break;
      }
    }
  }
  // To remove the root (minimum), swap values of root and last then removeLast
  // heapify down starting with the root until its right place
  void removeMin() {
    if (this->empty())
      return;
    // To remove root
    T.swap(T.root(), T.last());
    T.removeLast();
    // Heapify down
    Position par = T.root();
    while (T.hasLeft(par)) {
      Position mnChild = T.left(par);
      if (T.hasRight(par) && this->isLess(*T.right(par), *mnChild)) {
        mnChild = T.right(par);
      }
      if (isLess(*mnChild, *par)) {
        T.swap(par, mnChild);
        par = mnChild;
      } else {
        return;
      }
    }
  }

private:
  completeTree<E> T;
  C isLess;
  typedef typename completeTree<E>::Position Position;
};

Images from DSA in C++ book.